Ejercitación de lógica (2024-03-22)

1. Si la proposición es falsa, determine el valor de verdad de:

En este ejercicio se deben estudiar los casos por medio de tablas de verdad, y a parte de eso, se resuelve el valor de verdad. Se empieza con el supuesto de que es falso. Usando la tabla de verdad del condicional, considerando que la proposición es falsa, debería ser verdadero, y debería ser falso.

Después, con la tabla de negación en el término , concluimos que debe ser falso.

Luego, con el término , para que sea falso, necesitamos que sea verdadero. Según la tabla de la conjunción, y deberían ser mútuamente verdaderos. Por lo tanto deberá ser verdadero y, como vimos previamente deberá ser falso, siendo que está siendo negado.

Ahora, con la segunda proposición, determinaremos el valor de verdad de . Según la tabla de verdad del condicional, será verdadero, debido a que es falso y es verdadero, lo cual en la tabla define que la proposición será verdadera.

Con la tabla de la conjunción, veremos que la proposición será falso, y como tendremos un valor falso en el término y tenemos un condicional () en el siguiente termino, según su tabla, el valor de verdad será verdadero.

2. Determine si las siguientes expresiones son contradicciones, tautologías o contingencias.

• Crearemos una tabla de valor con cada proposición que compone a la principal.

V	V	V	F	F	F	V
V	F	F	F	V	V	V
F	V	F	V	F	V	V
F	F	F	V	V	V	V
Como todos los valores de la proposición compuesta son verdaderos, es una tautología.

• Drawing 2024-03-22 17.47.34.excalidraw

  ⚠ Switch to EXCALIDRAW VIEW in the MORE OPTIONS menu of this document. ⚠

  Text Elements

  Es contingencia

  Enlace al original

• Drawing 2024-03-22 18.03.11.excalidraw

  ⚠ Switch to EXCALIDRAW VIEW in the MORE OPTIONS menu of this document. ⚠

  Text Elements

  p

  r

  p

  r

  p

  p

  r

  p

  p

  r

  p

  p

  r

  r

  Es tautología

  r

  p

  Enlace al original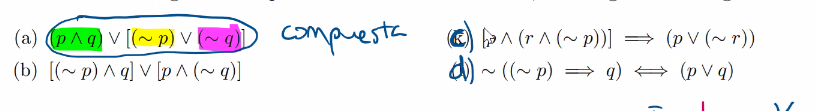

  

---

Clasificación de proposiciones compuestas

Sea una proposición compuesta (o función proposicional):

1. será una tautología si en la tabla de verdad de , el resultado siempre aparecerá verdadero (V).
2. será una contradicción si en la tabla de verdad de , el resultado siempre aparece falso (F)
3. es una contingencia si no es ni tautología, ni contradicción